PROTON IMPACT OF BIMOLECULAR TARGETS

Shadha J. Khalaf¹ --- Khalid A. Ahmad ²⁺ --- Riayhd K. A. Al-Ani³

^1,2,3 Department of Physics, College of Science, Mustansiriyah University, Baghdad, Iraq

Keywords:Hadron therapy, Organic compounds, Electronic excitation, DNA, Proton beams, Energy loss function., Liquid water

ARTICLE HISTORY: Received: 19 June 2017, Revised: 18 July 2017, Accepted:3 August 2017, Published: 2 10 August 2017

Contribution/ Originality: This study document an empirical method of obtaining the energy loss function which is the key quantity to study the energy deposited in targets of biological interest by swift projectiles such as protons, so it contains all the information about the electron excitation spectrum of the target.,. The model used through (ELF), namely the extended-Drude ELF. Each term in the sum of Drude-type functions has three adjustable parameters. The parameters a, b and c can be obtained by a fit of Eq. (1) to the ELF for compounds. Table 1 presents the determined three parameters in Eq. (1) for 5 compounds have been taken from reference [9]. The energy delivered by a swift proton beam in materials of interest to hadron therapy in 5 compounds is investigated.

1. INTRODUCTION

When high-energy radiation interacts with living tissue it produces a range of structural and chemical modifications that can affect biological function. These modifications occur via the production of intermediate species, which include excited atoms and molecules, radicals, ions, and secondary electrons [1]. To characterize energy delivered by the swift ions as a function of the depth by the Bragg curve, with a notorious peak nearly at the end of the trajectory, whose position and height based on projectile energy and target nature [2].

Besides the application to inert substances, the study of energetic projectiles interacting with materials of biological interest is also useful because they can be utilized in a controlled manner to kill malignant tumor cells [3].The use heavier ion such as proton beams for treating tumors lies in the reduced amount of energy deposited into healthy tissue in contrast with the higher dose delivered at the tumor location, and the well-defined range reached by the beam. Both characteristics are embodied in the depth–dose curve (commonly referred to as the Bragg curve), which represents the amount of energy delivered by the projectile as a function of the depth in the target [4].

In this paper we epitomize the formalism used to calculate, from the condensed matter point of view, the target probability, these analytical results are employed as input into the simulation in section 2.3 to enumerate Average electronic excitation energy and inverse inelastic men free path in section 2.5   think out mean excitation energy. Which are the main features of the energy deposited by a proton beam in materials currently used in hadron therapy treatment planning, such as liquid water, DNA, Poly (methyl methacrylate) (PMMA), Adenine and Guanine. Which are frequently utilized in hadron therapy remediation plans as tissue phantoms.

2. THEORETICAL BACK GROUND

2.1. Energy Loss Function

The dielectric approach has been acclimatized for describing the electron emission from liquid water and another compound induced by ion beams [5] its protraction to other relevant biological targets only was achieved very recently. The advantage of the dielectric formalism is that, provided that the ELF is experimentally known, many-body interactions and target physical-state effects are naturally included in the subsequent calculations [6].

The formula of dielectric function has a lot of importance to the content of the important guaranteed by the imaginary part that can be brokered account the energy lost of the different levels [7]. They can calculate the energy loss function ELF [8]:

Where the subscript “D"stands for Drude: ADi is the intensity. The extended form of Drude-formula is as follow Abril, et al. [10]:

Compound	formula	a(eV)3	b(eV)	c(eV)		B(eV)	P(g/cm3)
Water	H2O	3856.3	22.71	14.61	3.333	18.13	1.00
DNA	C20H27N7O13P2	5156.2	23.70	15.24	5.185	20.00	1.35
PMMA	C5H8O2	5399.2	23.70	15.57	3.600	20.00	1.188
Guanine	C5H5O1N5	6704.5	25.31	15.11	4.875	21.09	1.58
Adenine	C5H5N5	4885.7	24.32	12.78	4.667	20.44	1.35

Source: Tan, et al. [9]

2.2. Probability Per Unite Length

When fast projectile (proton) moves in substance material such as (liquid water, DNA and another compound) with mass M1, atomic mass Z1, kinetic energy T, and charge, it induces electronic excitations and ionizations in the material, losing energy in the process [12].  The probability per unite path length that a projectile with charge state q and energy T produces in the target an excitation of energy E=ħw irrespective of its momentum, ħk, (in a.u ħ=1)is given by Sabin and Oddershede [13].

2.3. Mean Excitation (Ionization) Energy

The mean excitation energy describes how easily a target, typically a molecule or atom can absorb kinetic energy from the projectile, primarily as electronic (inclusive ionization) and vibrational (including fragmentation) excitation. The mean excitation energy is characteristic of the target only, and has no dependence on the properties of the projectile ion. (One should note parenthetically that if the target is in an excited electronic state before the collision, the projectile might absorb energy from the target [18]. As the mean excitation energy enters the stopping power expression under the logarithm and in atomic units, small changes in mean excitation energies do not produce major changes in the stropping cross section [19].

Mean ionization energy required to remove a given electron from its atomic orbit and place it at rest at an infinite distance. The mean excitation is defined to be the mean value of the minimum energy transfer in a proton –atomic electron collision which produces an ionization event [20]. I is the ionization potential which, for considered system, is defined by Emfietzoglou, et al. [21]:

2.4. Average Electronic Excitation Energy Eav

To appreciate the possible damage induced in biological materials due to the irradiation with energetic particles, another interesting magnitude is the average energy Eav (T) transferred by a projectile of energy Tto the target producing electronic excitations and ionizations, which is defined by Pimblott and LaVerne [22]:

The average over all possible charge states (q = 0 and 1) in order to obtain the energy distribution, P(T, E), and the average energy Eav, of the electronic excitations produced in the target.

2.5. Inverse Inelastic Mean Free Path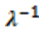

Proton inelastic mean free path is a characteristic quantity to describe the inelastic interactions of a charged proton with organic materials. It is essential importance this quantity in many fields of fundamental and applied research, like space radiation, shielding, radiation biology, and radiotherapy [23]. Monte Carlo track-structure calculations of charged particles represent a useful tool for the investigation of radiation effects on the radiated materials [24].

The calculations are based in the dielectric formalism, with a realistic description of the electronic properties of the target by the single Drude function,

3. RESULTS AND DISCUSSION

In this work (Eq. (3)) has been used as the key equation for all calculations. Additionally FORTRAN program has been written for our data analysis.

All parameters in (eq. (3)) are helped to evaluate the energy loss as function of incident proton in five compounds.

Fortunately, experimental information about the ELF in the optical limit, k = 0, exists for important biological materials, such as liquid water, DNA, PMMA, adenine, or Guanine. The Energy loss function ELF with different wave no k=0 to k=4.17 is show in fig. (1) for (a)  liquid water (b) DNA (c) Guanine (d) Adenine and (e) PMMA.

Fig-1. Energy loss function (ELF) of (a) H2O, (b) DNA, (c) Guanine (d) Adenine and (e) PMMA as a function of the transferred energy ħw, for several values of the momentum transfer ħk.

Source: this is our presentation work

Fig 2 shows the calculated probability per unit path length P (E,T), Eq. (3), for a proton beam (having incident energies T (0.25 ,0.5, 2.5, 5, 10 MeV)) at and of producing an electronic excitation of energy E in (a) H2O, (b) DNA, (c) Guanine (d) Adenine and (e) PMMA, and PMMA . The probability P (E,T) decreases as the proton energy T increases, indicating that a larger number of electronic excitations are produced when lower incident energies T are used, and at energy less than 20 eV, the probability P (T,E) increases as the excitation energy E increases as well.

Fig-2. Probability per unit path P for   projectile induces electronic excitation of energy E in (a) H2O, (b) DNA, (c) Guanine (d) Adenine and (e) PMMA at energy T=(0.25-10) MeV,  previous work [13].

Source: this is our presentation work

The ionization potential (I-value) of (a) H2O, (b) DNA, (c) Guanine (d) Adenine and (e) PMMA, are shown in table (2).

Our present results of ionization potential are compared with available previous work for dry DNA (I= 81.02 eV) [8] good agreement is achieved in previous work [16].

Table-2. The mean excitation energy for   projectile induces electronic excitation of energy T in H2O, DNA, Guanine, Adenine and (e) PMMA

Material	I (eV) calculated	I (eV) Expected	I (eV) Present work
DNA	86.64 [25]	90 [9]	81.02
Adenine	73.90 [25]	71.4 [9]	76.26
Guanine	78.25 [25]	75 [9]	77.01
PMMA	68.37 [9]	74 [9]	79.55
H2O	72.5 [9]	75 [9]	76.32

Source: this is our presentation work

Figure 3 shows Eav (T) as a function of the energy of a proton beam in liquid water, DNA, PMMA, adenine and Guanine with available previous data. We can observe that Eav (T) is rather similar for liquid water and DNA.

The mean energy Eav (T), given in Eq. (12), of the electronic excitations produced by a proton in DNA and another compound is depicted in Fig. (4). It is seen that Eav (T) increases with the proton energy T, being around 9-10 MeV in DNA and H2O, PMMA, Adenine or Guanine and around 69.48 eV for DNA, ≈66.3 eV, for H2O, ≈68.02 eV for PMMA, ≈ 69.09 eV for Adenine and ≈ 72.2 eV for Guanine. As the number of electronic excitations, the mean energy of the excitation increase with T. The results granted in Figs. (3)  and table 3 agree with  available previous work [10].

Table-3. The average energy for   projectile induces electronic excitation of energy T in H2O, DNA, Guanine, Adenine and (e) PMMA

Material	Eav (eV) Present work	Eav (eV) Previous work
DNA	69.48	63 [14]
Adenine	69.09	----
Guanine	72.2	----
PMMA	68.02	----
H2O	67.3	----

Source: this is our presentation work

Fig-3. Average energy Eav transferred by the projectile producing electronic excitations and ionizations in (a) H2O, (b) DNA, induced by a proton beam as a function of its energy. The calculations were obtained with the dielectric formalism the single Drude function. Circles correspond to results for ionization processes from a proton beam in DNA from Pimblott and LaVerne [22].

Source: this is our presentation work

We offered a methodology of estimating the IMFP of energetic proton in organic materials. Using this methodology we have performed the systematic calculations for the IMFP of 0.01–10MeV protons in a group of eleven important organic compounds, i.e. DNA, liquid water, PMMA, Adenine and Guanine.

The results in figure 4 obtain the inverse inelastic mean free path, or IIMFP, for protons in liquid water, and four organic compounds by using dielectric formalism in Eqs. (1). At proton energies lower than 1 MeV, sizeable differences between the inelastic mean free path corresponding to the five materials.

The maximum value of the inelastic mean free path, corresponding to proton energy ~ 0.1 MeV for the five biological materials DNA, H2O and Guanine, Adenine, and PMMA. The IIMFP in DNA is larger than in liquid water, whereas the IIMFP in PMMA is greater than in liquid water and compounds. IIMFP for H2O (0.145Å-1), DNA (0.162Å-1), Guanine is (0.165 A-1), for adenine is (0.159Å-1) and for PMMA is (0.147 A-1).

The results granted in Figs. (4)b for DNA agree with available previous work [26].

The purpose of this work is to give the proton inelastic MFP for these organic materials because of their importance in related radiation effect research and in space research. The data presented here are the first results of proton inelastic MFP for these bioorganic compounds over the energy range of 0.01–10MeV.

Fig-4. Inelastic mean free path (IMFP) results as a function of proton energy for (a) H2O, (b) DNA, (c) Guanine (d) Adenine and (e) PMMA.

Source: this is our presentation work

4. CONCLUSIONS

We have calculated the spectral distribution of the electronic excitations induced by a proton in liquid water, dry DNA and three compounds. For this purpose we use the dielectric formalism and obtain the target energy-loss function, Im from optical data to describe its extension to arbitrary values of momentum-transfer k, namely the extended-Drude We find that, regardless of the proton energy, the probability distribution P, of the electronic excitations has a maximum around 20 eV. Besides, P (E,T), which is related to the number of electronic excitations of a given energy E, decreases with the proton energy T. On the other hand the mean energy Eav of the electronic excitations increases monotonically with the proton energy T ranging from (10–20) eV at T = 0.01 MeV and around 10 eV for T = 10 MeV the mean energy of the excitation increases with T. This model examined agree in the calculation of P (T,E) and Eav at large values of the proton energy. At lower projectile energies important differences arise among the model. The mean excitation energy (I) of liquid water is estimated to be 72.5 eV. The inelastic MFPs for 0.05–10MeV protons in a group of 4 organic materials and water have been performed. The calculations are based on the method described in our previous work. The aim of this work is to present the proton IMFP for these organic compounds because of their importance in related radiation effect research and in space science.

Funding: This study received no specific financial support.

Competing Interests: The authors declare that they have no competing interests.

Contributors/Acknowledgement: All authors contributed equally to the conception and design of the study.

REFERENCES

[1]          I. Abril, R. Garcia-Molina, C. D. Denton, I. Kyriakou, and D. Emfietzoglou, "Energy loss of hydrogen and helium-ion beams in DNA: Calculation based on realistic energy-loss function of the target," Radiation Research, vol. 175, pp. 247–255, 2011.View at Publisher

[2]          H. Nikjoo, S. Uehara, D. Emfietzoglou, and A. Brahme, "Heavy charged particles in radiation biology and biophysics," New Journal of Physics, vol. 10, pp. 075006-1–075006-28, 2008. View at Google Scholar | View at Publisher

[3]          R. Garcia-Molina, I. Abril, I. Kyriakou, and D. Emfietzoglou, Energy loss of swift protons in liquid water: Role of optical data input and extension algorithms. In: Garcı´a Go´ mez-Tejedor, G., Fuss, M.C. (Eds.), Radiation damage in bio- molecular systems. Dordrecht: Springer, 2012.

[4]          R. Garcia-Molina, I. Abril, D. Emfietzoglou, P. De Vera, and I. Kyriakou, "A study of the energy deposition profile of proton beams in materials of hadron therapeutic interest," Applied Radiation and Isotopes, vol. 83, pp. 109-114, 2014. View at Google Scholar | View at Publisher

[5]          D. Emfietzoglou, "Inelastic cross-sections for electron transport in liquid water: A comparison of dielectric models," Radiation Physics and Chemistry, vol. 66, pp. 373-385, 2003.View at Google Scholar | View at Publisher

[6]          P. De Vera, I. Abril, R. Garcia-Molina, and V. S. Y. Andrey, "Ionization of biomolecular targets by ion impact:input data for radiobiological applications," Journal of Physics: Conference Series, vol. 438, p. 012015, 2013. View at Google Scholar | View at Publisher

[7]          G. Burns, Solid state physics, 1st ed.: Academic Press Inc., 1985.

[8]          P. De Vera, R. Garcia-Molina, I. Abril, and A. Solov’yov, "Semiempirical model for the Ion impact ionization of complex biological media," Physical  Review Letters, vol. 110, p. 148104, 2013. View at Google Scholar | View at Publisher

[9]          Z. Tan, Y. Xia, M. Zhao, X. Liu, F. Huang, and Y. Ji, "Electron stopping power and mean free path inorganic compounds over the energy range of 20–10,000 eV," Nuclear Instruments and Methods in Physics Research Section B, vol. 222, p. 27-43, 2004. View at Google Scholar | View at Publisher

[10]        I. Abril, D. Denton, P. De Vera, I. Kyriakou, D. Emfietzoglou, and R. Garcia Molina, "Effect of the Bethe surface description on the electronic excitations induced by energetic proton beams in liquid water and DNA," Nuclear Instruments and Methods in Physics Research Section B, vol. 268, pp. 1763– 1767, 2010. View at Google Scholar | View at Publisher

[11]        P. De Vera, E. Surdutovich, I. Abril, R. Garcia-Molina, and A. V. Solov’yov, "Analytical model of ionization and energy deposition by proton beams in subcellular compartments," European Physical Journal D, vol. 68, p. 96, 2014.View at Google Scholar | View at Publisher

[12]        I. Abril, R. Garcia-Molina, P. De Vera, I. Kyriakou, and D. Emfietzoglou, "Inelastic collisions of energetic protons in biological media. In: Belkic, Dz. (Ed.)," Elsevier Advances in Quantum Chemistry, vol. 65, pp. 129- 164, 2013. View at Google Scholar | View at Publisher

[13]        J. R. Sabin and J. Oddershede, "Stopping power—what next," Advances in Quantum Chemistry, vol. 49, p. 299-319, 2005.View at Google Scholar | View at Publisher

[14]        M. Barriga-Carrasco, D. Casas, and R. Morales, "Calculations on charge state and energy loss of argon ions in partially and fully ionized carbon plasmas," Physical Review E, vol. 93, p. 033204, 2016.View at Google Scholar | View at Publisher

[15]        Heradia-Avalos and R. Garcia-Molina, "Calculated energy loss of swift He, Li, B, and N ions in SiO2, Al2O3, and ZrO2," Physical Review A, vol. 72, p. 052902, 2005.View at Google Scholar | View at Publisher

[16]        P. De Vera, I. Abril, and R. Garcia Molina, "Inelastic scattering of electron and light ion beams in organic polymers," Journal of Applied Physics, vol. 109, pp. 094901-8, 2011.View at Google Scholar | View at Publisher

[17]        R. C. Fadanelli, C. M. Behar, L. C. C. M. Nagamine, M. Vos, N. R. Arista, C. D. Nascimento, R. Garcia-Molina, and I. Abril, "Energy loss function of solids assessed by Ion beam energy-loss measurements: Practical application to Ta2O5," Journal of Physical Chemistry C, vol. 119, pp. 20561–20570, 2015. View at Google Scholar | View at Publisher

[18]        A. Akar, H. Gumus, and N. T. Okumusoqlu, "Electron inelastic mean free path formula and CSDA-range calculation in biological compounds for low and intermediate energies," Applied Radiation and Isotopes, vol. 64, pp. 543-550, 2006.View at Google Scholar | View at Publisher

[19]        S. R. John, "Determination of the mean excitation energy of materials for projectile stopping power," Journal of Physical Chemistry and Biophysics, vol. 4, p. e118, 2014. View at Google Scholar | View at Publisher

[20]        H. Rong-Fu, "Mean excitation energy of the elements." Retrieved from https://www.osti.gov/servlets/purl/6733705/, 1973.

[21]        D. Emfietzoglou, M. R. Garcia, I. Kyriakou, I. Abril, and H. Nikjoo, "A dielectric response study of the electronic stopping power of liquid water for energetic protons and a new I-value for water," Physics in Medicine & Biology, vol. 54, pp. 3451-3472, 2009.View at Google Scholar 

[22]        S. M. Pimblott and J. LaVerne, "Production of low-energy electrons by ionizing radiation," Radiation Physics and Chemistry, vol. 76, p. 1244-1247, 2007. View at Google Scholar | View at Publisher

[23]        H. Nikjoo, S. Uehara, and D. Emfietzoglou, "Track structure codes in radiation research," Radiation Measurements, vol. 41, pp. 1052-1074, 2006. View at Google Scholar | View at Publisher

[24]        M. Kutz, Handbook of environmental degradation of materials. Norwich: William Andrew Inc., 2005.

[25]        Z. Tan, Y. Xia, M. Zhao, and X. Liu, "Proton stopping power in a group of bioorganic compounds over the energy range of 0.05– 10 MeV," Nuclear Instruments and Methods B, vol. 248, pp. 1–6, 2006. View at Google Scholar | View at Publisher

[26]        Z. Tan, Y. Xia, M. Zhao, and N. X. Liu, "Proton inelastic mean free path in a group of bioorganic compounds and water in 0.05–10 MeV range – including higher-order corrections," Nuclear Instruments and Methods in Physics Research Section B, vol. 268 p. 2337-2342, 2010. View at Google Scholar | View at Publisher